Ένα εκατομμύριο δολάρια θα κερδίσει όποιος καταφέρει να λύσει το διάσημο μαθηματικό πρόβλημα που βασανίζει τους μαθηματικούς για περισσότερο από έναν αιώνα. Πρόκειται για την υπόθεση Ρίμαν (Riemann hypothesis), που παρουσιάστηκε για πρώτη φορά από τον Γερμανό μαθηματικό Μπέρναρντ Ρίμαν (Bernhard Riemann) το 1859 και θεωρείται ένα από τα δυσκολότερα και πιο σημαντικά άλυτα προβλήματα των θεωρητικών μαθηματικών.
Το Ινστιτούτο Μαθηματικών Clay του Κέιμπριτζ της Μασαχουσέτης προσφέρει 1 εκατομμύριο δολάρια ΗΠΑ (σχεδόν 915.000 ευρώ) σε όποιον μπορεί να λύσει το «πρόβλημα της χιλιετίας», όπως έχει χαρακτηριστεί.
Η υπόθεση βασίζεται στη «συνάρτηση ζήτα» του Ρίμαν [ζ(s)]. Είναι μια συνάρτηση της οποίας το όρισμα s μπορεί να είναι οποιοσδήποτε μιγαδικός αριθμός εκτός του 1, και της οποίας οι τιμές είναι επίσης μιγαδικοί.
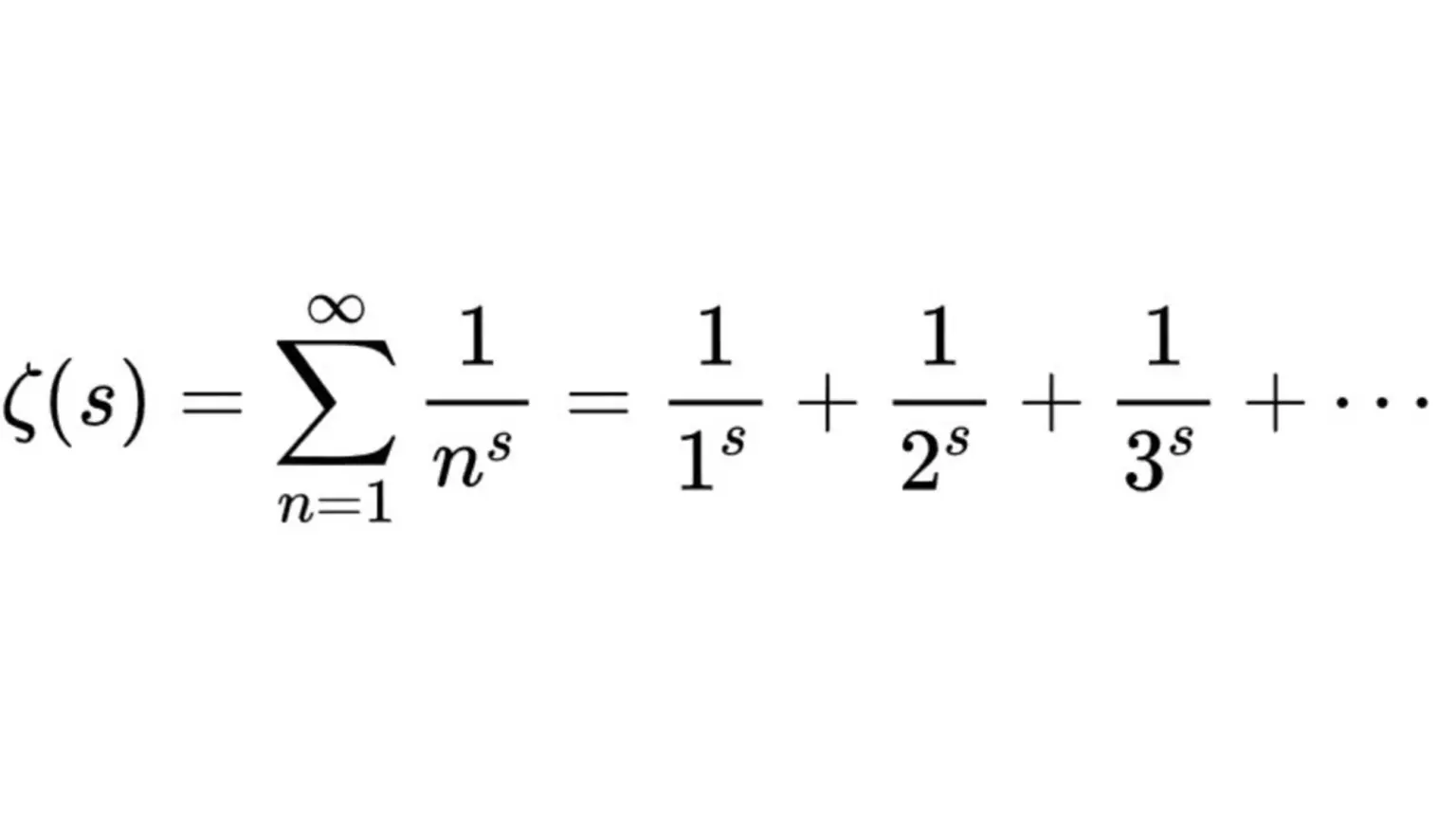
Έχει ρίζες τους αρνητικούς άρτιους αριθμούς; για τους οποίους ζ(s) = 0, όταν το s είναι ένας από τους -2, -4, -6, …. Αυτές ονομάζονται τετριμμένες ρίζες. Ωστόσο, ακόμη και οι αρνητικοί άρτιοι ακέραιοι δεν είναι οι μόνες τιμές για τις οποίες η συνάρτηση ζήτα είναι μηδέν. Οι άλλες ονομάζονται μη-τετριμμένες ρίζες. Η υπόθεση Ρίμαν αναφέρεται για τις θέσεις αυτών των μη τετριμμένων ριζών, και δηλώνει ότι:
Το πραγματικό μέρος κάθε μη τετριμμένης ρίζας της συνάρτησης ζήτα είναι 1/2. Έτσι, εάν η υπόθεση είναι σωστή, όλες οι μη τετριμμένες ρίζες βρίσκονται στην κρίσιμη γραμμή που αποτελείται από τους μιγαδικούς αριθμούς 1/2 + it, όπου t είναι ένας πραγματικός αριθμός και i είναι η φανταστική μονάδα.
Η απάντηση στην υπόθεση Riemann είναι ένα απλό «ναι» ή «όχι», αλλά υπάρχουν πολλοί υποθετικοί τρόποι για να φτάσετε εκεί και όλοι τους μέχρι σήμερα έχουν αποδειχθεί εξαιρετικά δύσκολη. Εάν η απάντηση είναι «ναι», θα είχε τεράστιες συνέπειες για τη θεωρία αριθμών, την κρυπτογράφηση και τη μελέτη των πρώτων αριθμών, γι’ αυτό η υπόθεση Riemann αποκαλείται και ως το «ιερό δισκοπότηρο των μαθηματικών».
Υπάρχουν πολλά καλά στοιχεία που οδηγούν τους μαθηματικούς να πιστεύουν ότι η υπόθεση Riemann είναι αληθής, αλλά χρειάζεται ακόμα να αποδειχθεί. «Έχει ελεγχθεί για τις πρώτες 10.000.000.000.000 λύσεις», λέει το ινστιτούτο για την υπόθεση Riemann. «Μια απόδειξη ότι είναι αληθής θα έριχνε φως σε πολλά από τα μυστήρια γύρω από την κατανομή των πρώτων αριθμών».
Από την άλλη, εάν η υπόθεση Riemann δεν είναι αληθινή, θα ανατρέψει πολλές από τις θεωρίες που έχουν δημιουργήσει οι άνθρωποι για τα μαθηματικά. Σύμφωνα με τη New York Post, όπως εξήγησε ο Νοτιοαφρικανός μαθηματικός Peter Sarnak: «Εάν (η Υπόθεση Riemann) δεν είναι αλήθεια, τότε ο κόσμος είναι ένα πολύ διαφορετικό μέρος… Κατά κάποιο τρόπο, θα ήταν πιο ενδιαφέρον αν ήταν ψεύτικο, αλλά θα ήταν καταστροφή γιατί έχουμε χτίσει τόσα πολλά γύρω από την υπόθεση της αλήθειας του».

































































